
First of all we replace the in the numerator by 0. Let us consider the -statistics in the case of the null hypothesis, i.e., let us see what happens to the value of when we assume that. This is hypothesis testing using the following null and alternative hypotheses: Case 2: Here we would like to test whether there is a significant difference between the population proportion. Where is the stardardised score with a cumulative probability of. The % confidence level for the difference in population proportions is given by: Thus we replace with and with in the standard deviation and obtain the following estimated standard error: We use as an estimate for and as an estimate for. The variance of is unknown as must be estimated in order to derive the confidence interval. The probability distribution of the difference in sample proportions is given by:Ĭase 1: We would like to find the confidence interval for the true difference in the two population proportions, that is. This follows from the fact that the sample elements are independent. Thus the distribution of the difference in sample proportions is normally distributed. Similarly, we can derive the probability distribution for, which is given by:įrom the theory of probability, a well-known results states that the sum (or difference) of two normally-distributed random variable is normally-distributed. (independently and identically distributed), then by the Central Limit Theorem, for sufficiently large, is normally distributed.
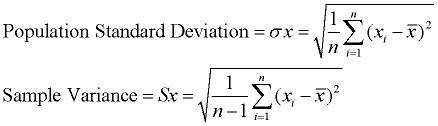
Since each is Bernoulli distributed with parameter, and assuming independence, then follows the binomial distribution with mean and variance. Let us first start with that for and the one for will follow in a similar fashion. Let us find the probability distributions of and. Note that each element in Sample 1 follows the Bernoulli distribution with parameter and each element in Sample 2 follows the Bernoulli distribution with parameter. We are going to assume that the sampled elements are independent (that is, the fact that a sample element is 1 (or 0) has no effect on whether another element is 1 or 0). Let be the sample proportion of successes for Sample 1. However we do not known the true values of the population parameters and, and hence we rely on estimates. Ĭase 1: A confidence interval for the difference in the (population) proportions, i.e., ,Ĭase 2: Testing the hypotheses whether or not the two (population) proportions are equal, or,Ĭase 3: Testing the hypotheses whether or not the two (population) proportions differ by some particular number. Let us also define to be the number of successes in Sample 1, i.e., and let be the number of successes in Sample 1, i.e. Similarly, Sample 2 is defined by the elements, and is the (true and unknown) population proportion for the elements found in Sample 2. That is, an element (for ) of Sample 1 has a probability of showing a value of 1 (i.e.
Let be the (true and unknown) population proportion for the elements found in Sample 1. Each element (for ) could take the value 1 representing a success or the value 0 representing a fail. Suppose that we have two samples: Sample 1 of size and Sample 2 of size. In the following we give a step-by-step derivation for the standard error for each case. Where is the size of Sample 1, is the size of Sample 2, is the sample proportion of Sample 1, is the sample proportion of Sample 2 and. Case 3: The standard error used for hypothesis testing of difference in proportions with is given by: Where is the pooled sample proportion given by where is the number of successes in Sample 1, is the number of successes in Sample 2, is the size of Sample 1 and is the size of Sample 2. Case 2: The standard error used for hypothesis testing of difference in proportions with is given by: Where is the size of Sample 1, is the size of Sample 2, is the sample proportion of Sample 1 and is the sample proportion of Sample 2. Case 1: The standard error used for the confidence interval of the difference in two proportions is given by: The following are three cases for the standard error. The standard error for the difference in two proportions can take different values and this depends on whether we are finding confidence interval (for the difference in proportions) or whether we are using hypothesis testing (for testing the significance of a difference in the two proportions).

What is the standard error of the difference in two proportions?


 0 kommentar(er)
0 kommentar(er)
